介绍
该项目地址为radio_receiver, 是Jacobo Tarrío开发的一个Chrome插件(不~应该是应用), 开源, 不依赖外部库, 只需要Chrome和这个应用以及硬件就可以工作. 亲测用起来很爽.
该项目的很简单, 只有两个文件夹, 程序都集中在extension中. 这一堆.js是java script吧? 这玩意都发展到如此强大的地步了?
概览
首先我觉得奇怪的是它如何实现与USB通讯的? 没有DLL么? 在rtl2832u.js中什么也没找到, 在rtlcom.js中找到这一段
... line 280
/**
* Sends a USB control message to write to the device.
* @param {number} value The value field of the control message.
* @param {number} index The index field of the control message.
* @param {ArrayBuffer} buffer The buffer to write to the device.
* @param {Function} kont The continuation for this function.
*/
function writeCtrlMsg(value, index, buffer, kont) {
var ti = {
'requestType': 'vendor',
'recipient': 'device',
'direction': 'out',
'request': 0,
'value': value,
'index': index,
'data': buffer
};
chrome.usb.controlTransfer(conn, ti, function(event) {
...
Chrome内置了usb接口, 好吧~
Jacobo Tarrío对文件名的命名很易懂, 我顺利的找到了demodulator-wbfm.js. 超级简单的一个函数.
/**
* Demodulates the signal.
* @param {Float32Array} samplesI The I components of the samples.
* @param {Float32Array} samplesQ The Q components of the samples.
* @param {boolean} inStereo Whether to try decoding the stereo signal.
* @return {{left:ArrayBuffer,right:ArrayBuffer,stereo:boolean,carrier:boolean}}
* The demodulated audio signal.
*/
function demodulate(samplesI, samplesQ, inStereo) {
var demodulated = demodulator.demodulateTuned(samplesI, samplesQ); //这应该是FM解调
var leftAudio = monoSampler.downsample(demodulated); //左声道(L+R)先只做一个抽取
var rightAudio = new Float32Array(leftAudio); //右声道是左声道的copy
var stereoOut = false;
if (inStereo) { //如果设置了要解调立体声
var stereo = stereoSeparator.separate(demodulated); //立体声解调
if (stereo.found) {
stereoOut = true;
var diffAudio = stereoSampler.downsample(stereo.diff); //抽取L-R
for (var i = 0; i < diffAudio.length; ++i) {
rightAudio[i] -= diffAudio[i]; //做L与R分离
leftAudio[i] += diffAudio[i];
}
}
}
leftDeemph.inPlace(leftAudio); //去预加重
rightDeemph.inPlace(rightAudio);
return {left: leftAudio.buffer,
right: rightAudio.buffer,
stereo: stereoOut,
signalLevel: demodulator.getRelSignalPower() };
}
OK, 清晰明了, 那么我们开始挨个研究吧~
demodulator.demodulateTuned - FM解调
该函数位于dsp.js文件中line 345.
这一段为FM的解调算法, 省略了一开始的抽取, 输入为I与Q, 一进来先抽取, lI和lQ为Last I与Q的意思.
var real = lI * I[i] + lQ * Q[i];
var imag = lI * Q[i] - I[i] * lQ;
这个算法是和阅读librtlsdr中的rtl_fm程序中用的方法完全一致, 也就是FM解调方法中的方案2: 求角度差->atan2. 详细情况见第一篇文章中的分析.
那么接下来是求atan2, 但atan2是很费cpu的, 因此Jacobo似乎是用了近似的方法, 因此先根据real和imag的值来判断角度在哪个象限, 然后再进行估算.
var sgn = 1; //sqn初始化为0~180
if (imag < 0) { //这时角度>180
sgn *= -1; //用sqn记住这是个负角度
imag *= -1; //转为180度以内的, 下面的算法应不能算超过180度
}
var ang = 0;
var div;
if (real == imag) { //此时为45度, 省一次除法-_-
div = 1;
} else if (real > imag) { //注意imag肯定是>0的, 那么是小于45度的情况
div = imag / real;
} else { //imag>real,45度至179度.
ang = -Math.PI / 2; //在45度~90度的范围也需要+90度?
div = real / imag; //这是这种算法在后边象限的普遍选择
sgn *= -1; //已晕
}
代码里的公式略复杂, 我重写如下:
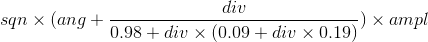
为什么是45度~180度范围? 我查到的别的资料都是从90度开始的, 我不知道是我看的有问题还是Jacobo的算法有问题, 于是我打算验证一下. 于是我就把这个算法放到python里和np.angle()函数做了下对比.
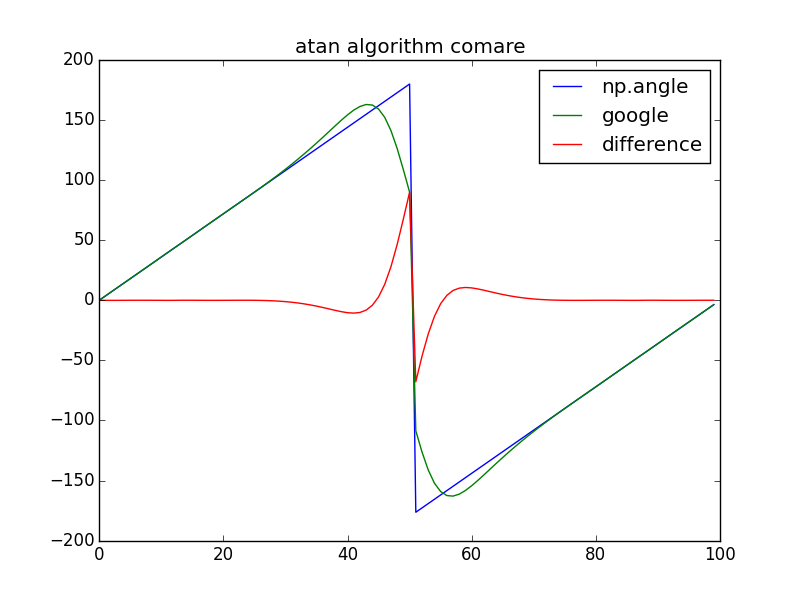
横轴是测试点, 纵轴为角度, 在0~360范围内共测试100个点, 可以看到在超过180度后, 转为-180, 而Jacobo的逼近算法在180度左右位置的误差最大, 可达到近100度, 但这也是线性拟合这种非线性函数的缺点(本人数学白痴, 说错了请指正). 但该算法在小于90度的范围内几乎是完全一致的.
至于为什么这个算法是这么算的, 我查了几个atan拟合的算法, 和这个不太一样.
一般的选择都是在90度的位置用if分开, 但Jacobo确是在45度, 当然这和后边的多项式有关. 这应当是设计时有考虑吧.
后来我发现了作者的blog中有关于FM解调的内容, 但可惜他没有细说.经过谷歌翻译的Amplitude modulation and frequency modulation
OK, 我们继续.
StereoSeparator.separate - 立体声解调
这里省掉了抽取的程序. 这段程序的输入为FM解调后的信号. 输出为L-R信号. 那么就是说内部应是进行了乘38k的过程.
... line 404
var iavg = new ExpAverage(9999);
var qavg = new ExpAverage(9999);
var cavg = new ExpAverage(49999, true);
...
... line 492
function ExpAverage(weight, opt_std) {
var avg = 0;
var std = 0;
/**
* Adds a value to the moving average.
* @param {number} value The value to add.
* @return {number} The moving average.
*/
function add(value) {
avg = (weight * avg + value) / (weight + 1);
if (opt_std) {
std = (weight * std + (value - avg) * (value - avg)) / (weight + 1);
}
return avg;
}
...
这三个是平均的函数(本人OOP盲, 名词不懂见谅), 9999这个平均参数好大~, 平均的方法很简单.
... line 408
for (var i = 0; i < 8001; ++i) {
var freq = (pilotFreq + i / 100 - 40) * 2 * Math.PI / sampleRate;
SIN[i] = Math.sin(freq); //pilotFreq=19000
COS[i] = Math.cos(freq); //sampleRate=336000
}
...
这段程序令我感到很困惑, 按理说这程序应是初始化SIN和COS这两个查找表的吧? 以便后边不用算cos和sin, 但其算法很奇怪,
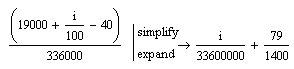
简化后的式子如上图, 也就是说这是一个 (1/33600000)个周期/样本 的正弦波, 且滞后0.056弧度. 也就是说, 8000个样点只是这个正弦波的很小一部分(0.02%), 于是我画了一下, 这就是斜线么~ 好吧我先看看别的. 画图程序:
import numpy as np
from pylab import plot,subplot
i=np.arange(0,8000)
freq=(19000+i/100-40)*2*np.pi/336000
sin=np.sin(freq)
cos=np.cos(freq)
subplot(2,1,1)
plot(sin)
subplot(2,1,2)
plot(cos)
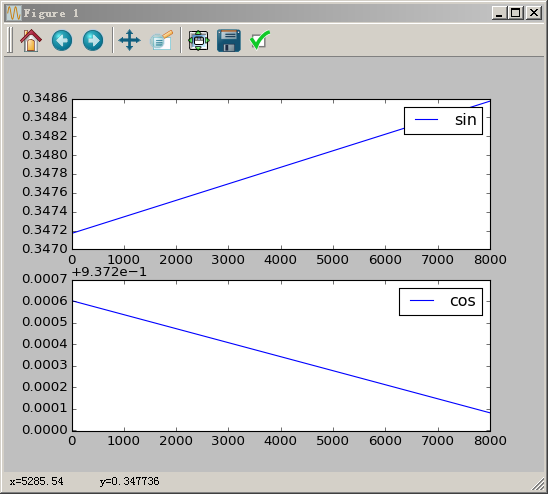
图, 为啥cos那幅图的y轴自动减了? 方便看么?
... line 422
out[i] *= sin * cos * 2;
...
函数的输出是这样计算的. (图来自wiki)
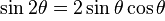
这是恒等式嘛~也就是让out乘上38k的意思, 那也就是说之前已经搞定19k了. 那我们完整的看一下.
var corr; //调整用参数
if (hdev > 0) {
corr = Math.max(-4, Math.min(4, vdev / hdev));
} else {
corr = vdev == 0 ? 0 : (vdev > 0 ? 4 : -4); //vdev=0
}
var idx = Math.round((corr + 4) * 1000);
这部分应当就是鉴相部分, 判断相位差目前是多少, 且根据相位差来调整本振的相位. 但这个vdev和hdev的得出令人困惑.
var hdev = iavg.add(out[i] * sin);
var vdev = qavg.add(out[i] * cos);
9999的平均, 采样率336k, 那么对于19k的信号, 一个周期有17.7个sample. 那么9999的平均应当完全将sin和cos拉平才对.
此时我翻到了作者的blog经谷歌翻译的How demodulate FM stereo radio, 作者介绍的方法是类PLL法, 首先检测19k的相位, 然后调整一个VFO.
还是完全不明白的我没办法, 就只能上大招了. 我在chrome里调试看看实际是怎么算的可以吧? 这调试界面真是先进啊, 搞这么多年单片机还没用过这么自动化的. 你看一设断点变量都自动显示出来了.
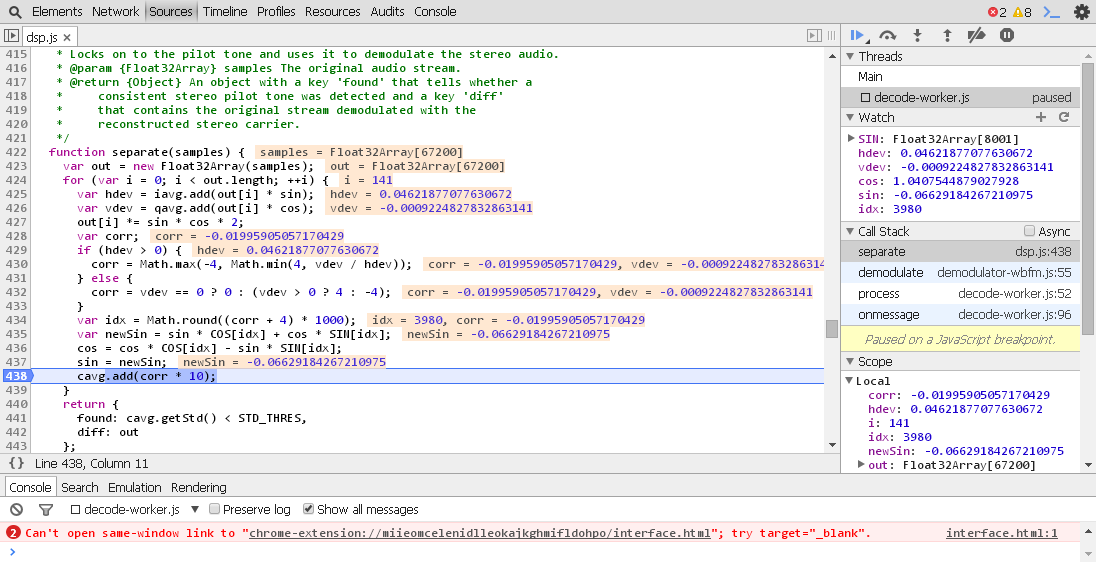
然后证实了sin和cos确实是一个差不多18个sample每周期的信号, 而初始化的那个SIN[]和COS[]也确实是个斜线. 然后第二日的早晨, 我这脑袋忽然开窍了, out[i] * sin 我去这不是求19k的相位差的方法吗? 见关于US6901146的描述FM立体声解调方法研究 19k的本振乘上输入(包含L+R,L-R,19k), 结果就是低频以及DC成分就是两个19k的相位差, 因此根据这个来调整本振就可以了. 也就是说, hdev和vdev分别是本振I和Q的相位差, 而average就是所谓的LPF. 附上用到的三角恒等式.
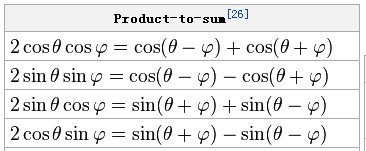
var idx = Math.round((corr + 4) * 1000);
var newSin = sin * COS[idx] + cos * SIN[idx];
cos = cos * COS[idx] - sin * SIN[idx];
sin = newSin;
那么鉴相部分就是根据这个差来调整COS和SIN的index, 从而调整这个NCO的频率. 那么问题是, 那近似直线的斜线如何实现调整频率的?
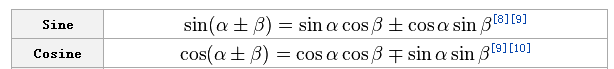
我觉得这就是答案, β是每次sin和cos向前增加的角度. 而之前那个斜线就是可调整的每次增加的量. 那么那个函数应该这样理解. 程序重贴在下面.
... line 409
var freq = (pilotFreq + i / 100 - 40) * 2 * Math.PI / sampleRate;
...
这段程序生成的应是在19k的频率下, 向前步进的步长. 而这个步长, 就是在此采样率下频率由18.96k~19.04k范围变化时一个采样大小的角度, 也就是说可容忍的本振与副载波频率之间的差最大为±40Hz. OK, 那回去看看鉴频部分的工作方式.
...
var hdev = iavg.add(out[i] * sin);
var vdev = qavg.add(out[i] * cos);
...
var corr; //调整用参数
if (hdev > 0) {
corr = Math.max(-4, Math.min(4, vdev / hdev)); //>0, 意味着
} else {
corr = vdev == 0 ? 0 : (vdev > 0 ? 4 : -4);
}
var idx = Math.round((corr + 4) * 1000);
...
vdev和hdev是与输入19k的相位差, 见下面的恒等式, 相乘并LPF后, 留下的是差. 首先假设输入为sin, 那么hdev就是cos(差), vdev就是sin(差).
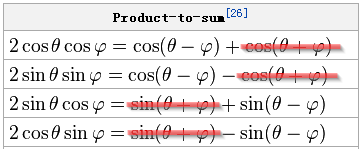
参照下图来看这个表格.
| cos(x) <= 0 | 此时hdev <= 0 |
|---|---|
| sin(x) = 0 | 应是用于一开始的第一个点 |
| sin(x) > 0 | 此时角度位于90度~180度, 超过范围, 则是4 |
| sin(x) < 0 | 此时角度为-180度~-90度, 为-4 |
| cos(x) > 0 | 此时hdev > 0 |
| sin/cos=tan | 此时是-90~90度范围, vdev/hdev |
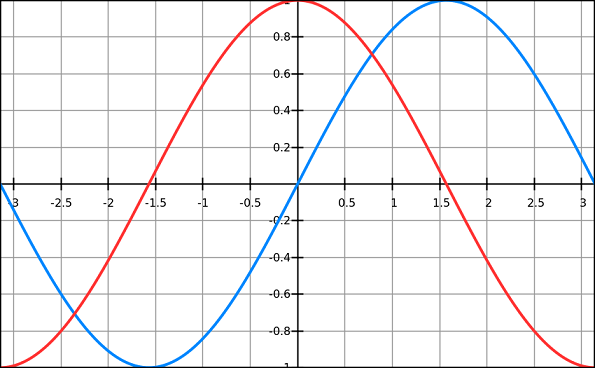
也就是说, 这段程序只将-90~90度之间的范围映射到±40Hz的范围上, 大于90度的范围固定为4, 小于-90度的范围固定为-4. 而范围内的角度, 一般是要计算arctan来得到角度, 但由于index范围受限, 因此限制在4以内, 而在这个小范围内求arctan, 没有必要, 因为也不需要求得角度的精确值, 因此就用这个tan来近似线性的频率变化. 可以参考下图.
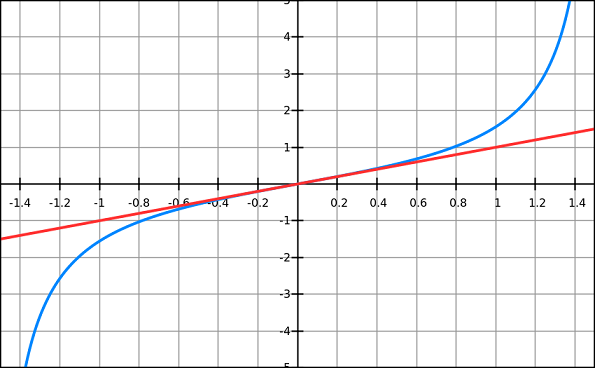
总结
FM解调的方法: 求角度差->求arctan, 这里arctan是用的近似的算法.
立体声解调: 总的来说是PLL法, 但实现的方法比较特别.
Jacobo作为一个google的js工程师真是厉害呀, 果然去google工作的都是牛人.
Comments
comments powered by Disqus